Yuhai Tuの論文を読み解く-03

・式 [4]の下，p.14856，左段落，上から二行目

\( \Large \displaystyle f_L([L]) = ln \left( 1 + \frac{{L}}{K_I} \right) -ln \left( 1 + \frac{{L}}{K_A} \right) \)

を読み解きましょう．これを読み解く上で参考になるのは，

Quantitative Modeling of Bacterial Chemotaxis: Signal Amplification and Accurate Adaptation
Yuhai Tu, Annu Rev Biophys. 2013; 42: 337–359.

です．

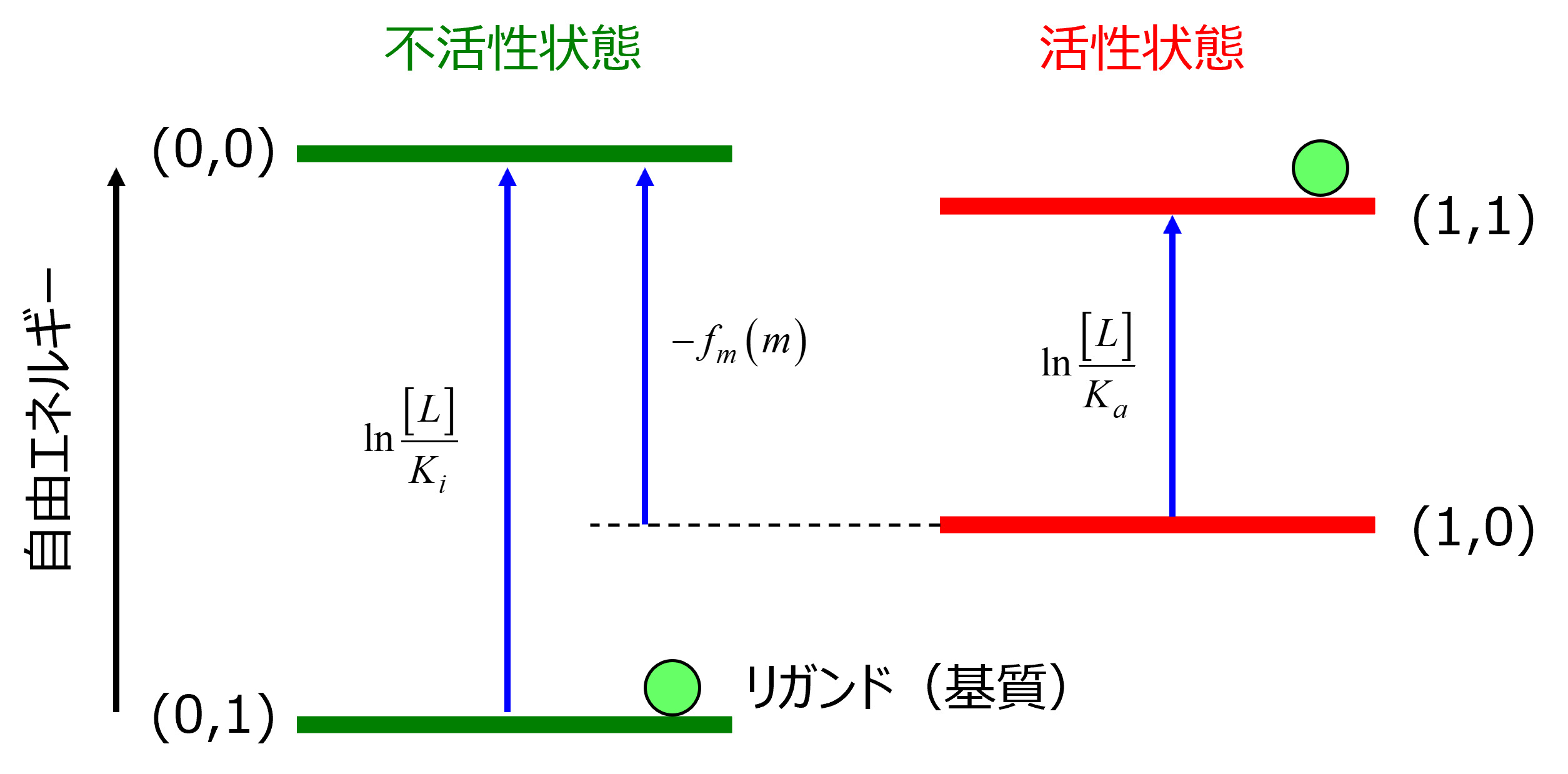
その中の図（論文の図をそのまま掲載すると著作権に引っかかりますので，まねてみました．

ここでは，
　P（0，0）　：　不活性，　リガンド未結合
　P（0，1）　：　不活性，　リガンド結合
　P（0，0）　：　活性，　　リガンド未結合
　P（0，0）　：　活性，　　リガンド結合

の4状態を考えます．リガンドが結合していても活性，という場合もあるのですね．

ここで，不活性（もしくは活性）状態の自由エネルギー差は，ここで，記載したとおり，

\( \Large \displaystyle E_{on} = E_{off} + ln \left( \frac {K}{L} \right) \)

\( \Large \displaystyle E_{off} = E_{on} - ln \left( \frac {K}{L} \right) = E_{on} + ln \left( \frac {L}{K} \right)\)

となります．

活性（もしくは不活性）状態のみの二状態を考えると，

\( \Large \ce{R <=>C[k_{+} L][k_{-}] RL} \)

となり，平衡状態においては，

\( \Large k_+ \cdot R \cdot L = k_- \cdot RL \)

解離定数は，

\( \Large \displaystyle K = \frac{k_-}{k_+} = \frac{R \cdot L}{RL} \)

となります，二状態の割合は（不活性状態においては），

\( \Large \displaystyle \frac{RL}{R} = \frac{P(0,1)}{P(0,1)} = \frac{L}{K} \)

となります，四状態それぞれでは，

\( \Large \displaystyle \frac{P(0,1)}{P(0,1)} = \frac{L}{K_i} \)

\( \Large \displaystyle \frac{P(1,1)}{P(1,1)} = \frac{L}{K_a} \)

\( \Large \displaystyle \frac{P(1,0)}{P(0,0)} = e^{-f_m (m)} \)

最後の式は，ここ，で導出しています．

この四状態で保存則が成り立ちますので，

\( \Large \displaystyle P(0,0) + P(0,1) + P(1,0) + P(1,1) = 1 \)

\( \Large \displaystyle P(0,0) \left\{ 1 + \frac{L}{K_i} \right\} + P(1,0) \left\{ 1 + \frac{L}{K_a} \right\}= 1 \)

\( \Large \displaystyle e^{f_m (m)} \cdot P(1,0) \left\{ 1 + \frac{L}{K_i} \right\} + P(1,0) \left\{ 1 + \frac{L}{K_a} \right\}= 1 \)

\( \Large \displaystyle P(1,0) = \frac{1}{e^{f_m (m)}\cdot \left\{ 1 + \frac{L}{K_i} \right\} + \left\{ 1 + \frac{L}{K_a} \right\}} \)

\( \Large \displaystyle P(1,1) = \frac{ \frac{L}{K_a}}{e^{f_m (m)}\cdot \left\{ 1 + \frac{L}{K_i} \right\} + \left\{ 1 + \frac{L}{K_a} \right\}} \)

となります．

活性状態の割合は，

\( \Large \displaystyle <a> = \sum_{a=0}^1 \sum_{l=0}^1 a \cdot P(a,l) = P(1,0) + P(1,1) \)

\( \Large \displaystyle = \frac{1}{e^{f_m (m)}\cdot \left\{ 1 + \frac{L}{K_i} \right\} + \left\{ 1 + \frac{L}{K_a} \right\}} + \frac{ \frac{L}{K_a}}{e^{f_m (m)}\cdot \left\{ 1 + \frac{L}{K_i} \right\} + \left\{ 1 + \frac{L}{K_a} \right\}} \)

\( \Large \displaystyle = \frac{ 1 + \frac{L}{K_a}}{e^{f_m (m)}\cdot \left\{ 1 + \frac{L}{K_i} \right\} + \left\{ 1 + \frac{L}{K_a} \right\}} \)

\( \Large \displaystyle <a> = \frac{ 1 }{1 + e^{f_m (m)} \cdot \frac{ 1 + \frac{L}{K_i}}{ 1 + \frac{L}{K_a}} } \)

\( \Large \displaystyle <a> = \frac{ 1 }{1 + exp \left[ f_m (m) + ln \frac{ 1 + \frac{L}{K_i}}{ 1 + \frac{L}{K_a}} \right]} \)

活性状態の割合は，ここ，にあるように，

\( \Large \displaystyle = \frac{1}{1 + exp \left( \Delta E \right)} \)

となるので，

\( \Large \displaystyle \Delta E = - f_m (m) - ln \frac{ 1 + \frac{L}{K_i}}{ 1 + \frac{L}{K_a}} \)

となります．

右辺第一項はメチル化，ｍ，の関数，第二項はリガンド濃度，L，の関数となりますので，

\( \Large \displaystyle - f_m (m) - ln \frac{ 1 + \frac{L}{K_i}}{ 1 + \frac{L}{K_a}} = -f_m (m) - f_L (L) \)

なので，

\( \Large \displaystyle f_L (L) = ln \frac{ 1 + \frac{L}{K_i}}{ 1 + \frac{L}{K_a}} = ln \left( 1 + \frac{L}{K_i} \right) - ln \left( 1 + \frac{L}{K_a} \right)\)

となり，最初の式を導き出せました（添え字が大文字になったり小文字になったりしていますが．．．．）